This is a runbook on setting up redundant storage on Windows.

More precisely, even the best neural networks can not be trained to approximate periodic functions using stochastic gradient descent. (empirically, prove me wrong!)

Contents

• Simulating a clock
• Simplifying the problem
• Why can’t we train the sin?
• What to do about it?

Simulating a clock

The problem that led me into this sinkhole is an attempt to model biological rhythms. People sleep every 24 hours, the nature has a distinct 365 day cycle, and over a month the Moon goes from new to full and back. I wanted to capture that repetition relative to the current instant in time, which led to the Clock Problem:

Given the number of seconds since some moment T0 defined to be 0 days 0:00:00, train a neural network to approximate the numbers you would see on a digital clock. For example, -1 (second) would be 23:59:59.

Expecting that to be a dead simple task, I built an infinite dataset, that would sample a random instant in time from a period of 120 years, and fed it into a SIREN - neural network with sinusoidal activations.

To my surprise, despite playing with its frequency scale hyperparameter, the network, essentially, never converged.

I tried to use regular MLP with GELU activations, and got approximately the same result.

Research on the topic only brought Neural Networks Fail to Learn Periodic Functions and How to Fix It, which, as you might have guessed it, did not really work on the Clock Problem. Their x + sin(x) ** 2 activation only really worked when the number of full cycles in the dataset was less than the number of paramters of the network, which completely misses the point.

Simplifying the problem

You can quickly see how inappropriate gradient descent is for the problem if we just simplify it a little. Let’s try approximating this trivial function:

FREQUENCY_SCALE = 31

def func(x):
    return torch.sin(x * FREQUENCY_SCALE)

There is a a PyTorch module, that surely should solve the problem:

class Sin(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.freq = torch.nn.Parameter(torch.randn(1))

    def forward(self, x):
        return torch.sin(self.freq * x)

Here, we only need to find the frequency, and the module will match our target function exactly! Let’s try it out:

net = Sin()
opt = torch.optim.SGD(net.parameters(), lr=0.0001)

BATCH_SIZE = 32


for batch_idx in range(1000*1000):
    opt.zero_grad()

    batch = (torch.rand(size=[BATCH_SIZE, 1], device=device) * 2 - 1) * 1000

    out = net(batch)
    expected = func(batch)

    loss = ((out - expected) ** 2).mean()

    loss.backward()

    opt.step()

    if batch_idx % 1000 == 0:
        print(f'{loss.detach().cpu().item()}')

If you run this on your machine, you will see something like this:

0.775499165058136 1.3729740381240845 1.0878400802612305 0.7583212852478027 1.3061308860778809 0.6976296305656433 1.0671122074127197 0.9739978909492493 0.947789192199707

The loss just floats around 1 and never converges.

But we actually know the answer! Just insert this line:

net.freq.data = torch.tensor([31], dtype=torch.float32)

and your loss will turn to zero instantly:

0.0 0.0 0.0 0.0

Why can’t we train the sin?

For the given x0 the derivative of our scaled sin with respect to freq parameter is x0 * cos(x0 * freq). There are two things to note:

1. The scale of the derivative value depends on how far x0 is from 0. This is bad, as really that dependency only makes sense within [-x0/freq*pi, +x0/freq*pi] interval.
2. The derivative does not really point where we want to go. Instead, its direction only depends on whether the x0 * freq is closer to 2n*pi or (2n+1)*pi for some n. And that value will vary wildly for different samples in the batch.

This is how the gradient of the freq paramter looks like on a large random batch of points:

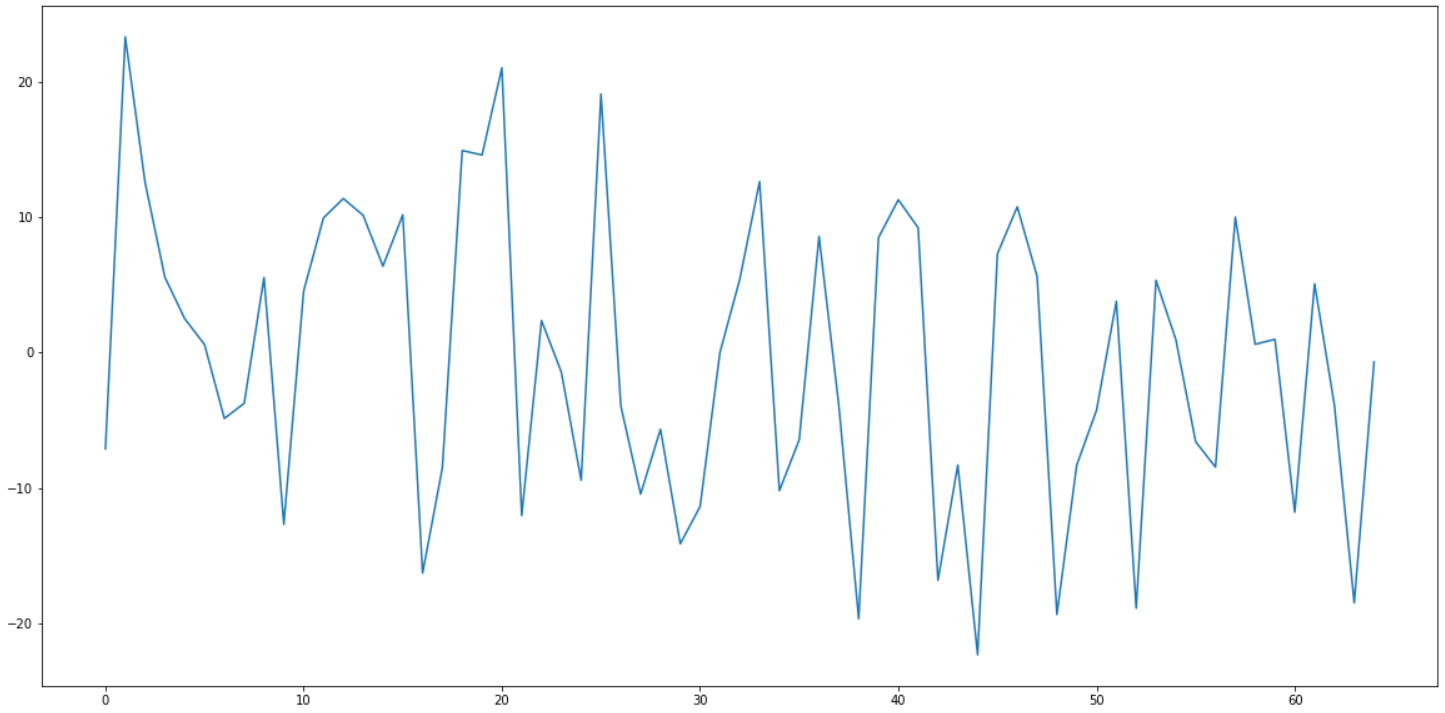
Can you spot the 0 at 31? As you can see, around it the gradient is all over the place.

Even in the immediate vicinity of 31, it does not behave well:

What to do about it?

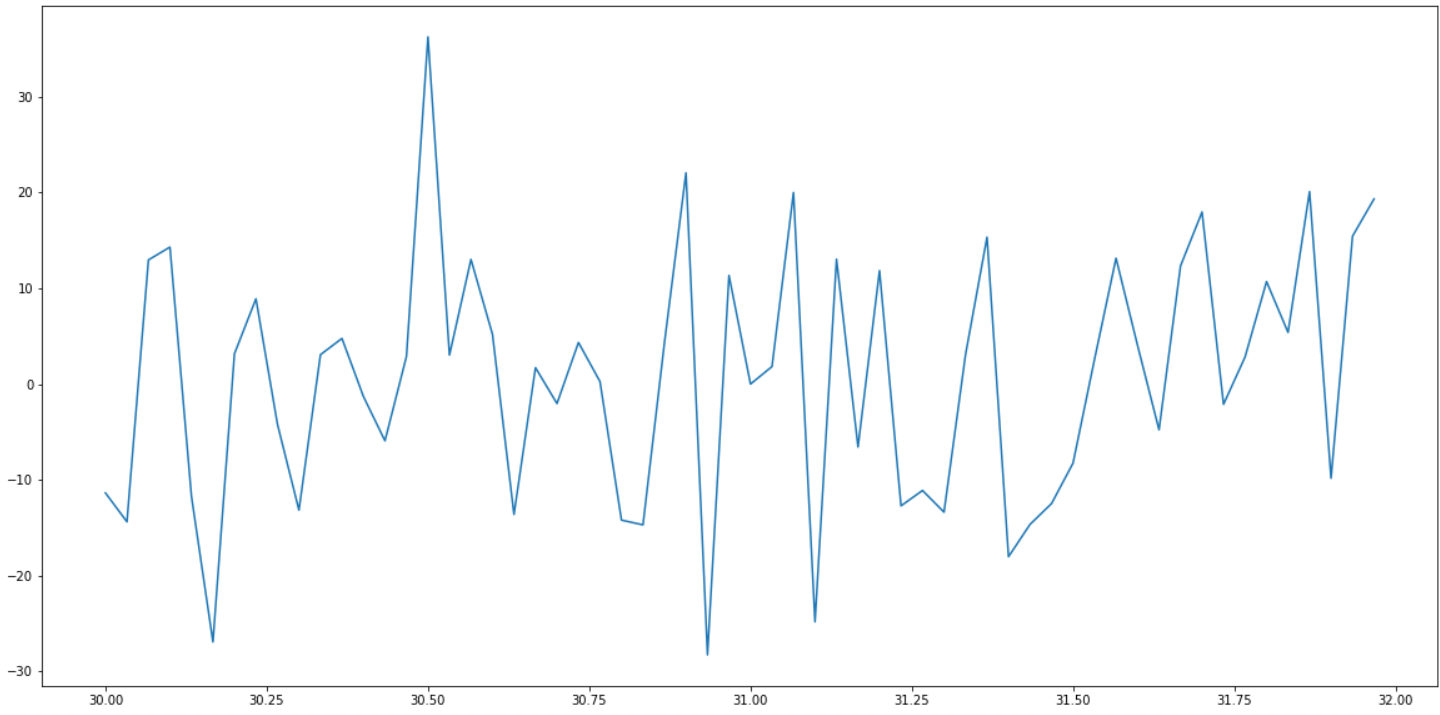
I don’t know. Perhaps a form of Fourier transform or a wavelet transform would help. Time to beef up on signal processing.

Privacy is hard these days. Tech companies want to know everything about you to show more and more advertisement, or to sell the data to the third parties, who then resell to the next ones, then further, until a a toy vendor knows more about your kids, than you do.

The app permission systems, that became popular with Android and iOS are a godsend. Now your bookreader app does not know your location, who your friends are, and can’t upload your private photos to their servers as a part of “analytics telemetry”.

Microsoft introduced a similar system with Windows 8 for the apps installed from the Microsoft Store, and expanded it in Windows 10 to any app packaged in a special way. So when you install an app from Store, you can be reasonably sure, that it does only what it is supposed to, right? Not so fast!

Today I was notified, that it is no longer possible to submit updates to my user-friendly Ethereum miner to Windows Store due to the new Microsoft policies.

What a shame.

UPD. You can now reinstall miner from Lost Tech Downloads

Had to switch to Brave today, as Chromium has not been getting new versions on Chocolatey, which is a security issue. It is stuck at v75 while v76, v77, and v78 have been out for a while.

A story of lost and recovered code for a project I just created.

In Silicon Valley season 4, Jian-Yang builds an AI app that identifies pictures of hotdogs. Today I am going to make a similar app to identify C# from code fragments (in case you forget how C# looks like!).

Look at this Python trying to pretend to be your favorite language:

var = await.add(item)
switch(hello)

Of course the whole thing from building and training a deep convolutional network to the cross-platform UI will be written in .NET + TensorFlow.

Advanced-level tutorial on training a deep convnet to classify language from code fragments

C# occupies a lot of horizontal space. Pretty much every file has a namespace, which by default adds 4 characters, and then another 4 characters from the actual class you are trying to define.

How often do you look at the code you wrote ~10 years ago? Bitbucket announced Sunsetting Mercurial Support, including complete removal of all repositories using that source control system. So naturally, as one of the unfortunate souls who initially picked HG over Git, I checked out what I had there.

<!DOCTYPE html>